K-means by another means
Wait. Does k-means count as machine learning? Yes. Yes, it does.
CS229 is the graduate-level machine learning course I took at Stanford as part of the Graduate Certificate in AI which I received back in 2021. While k-means is my choice as the easiest to understand algorithm in machine learning, it was taught as the introductory clustering algorithm for unsupervised learning. As a TA for XCS229, which I have been doing since 2022 and most recently did this Spring, I know that it is still being taught as part of this seminal course in AI.
We have liftoff!
Unlike previously where I saved the result for the end, let’s start by taking a look at the algorithm in action!
Here is a screenshot of the final decision boundary after convergence.
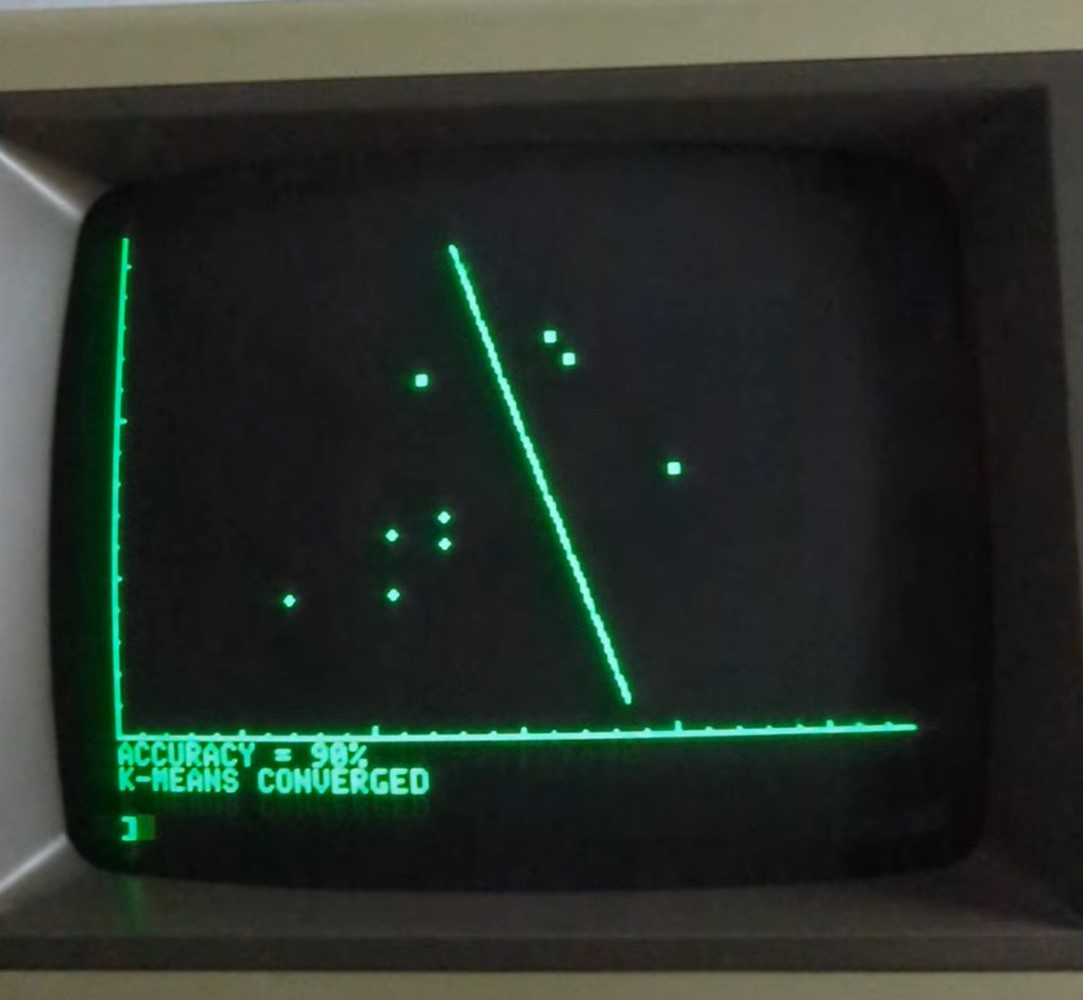
The final accuracy is 90% because 1 of the 10 observations is on the incorrect side of the decision boundary.
For debugging purposes, to speed up execution, I reduced the number of samples in each class to 5. (You might note that, on the graph, there are only 4 points in class 1, which are the □s. That’s because one of the points is at (291, 90), which is off the edge of the screen. Gaussian distributions can generate extreme outliers, so I decided to preserve those points rather than clip them to the edge of the screen.) That’s obviously pretty small but you can see the algorithm iterating.
At the end of each loop I draw a line between the latest estimates of cluster centroids. The perpendicular bisector of these segments are the decision boundaries between the classes, so I draw them, too. Some of the code was written to handle more than two classes but here there are only two which makes this relatively easy.
K-means explained
K-means clustering is an iterative algorithm that aims to partition \(n\) observations into \(k\) clusters in which each observation belongs to the cluster with the nearest mean, called the cluster centroid.
| Step | Description |
|---|---|
| Initialize | Produce and initial set of k cluster centroids. This can be done by randomly choosing k observations from the dataset. |
| Step 1 - Assignment | Using Euclidean distance to the centroids, assign each observation to a cluster. |
| Step 2 - Update | For each cluster, recompute the centroid using the newly assigned observations. If the centroids change (outside of a certain tolerance), go back to step 1 and repeat. |
Ezpz.
The math is also simple. In step 1, the distance between two points, \(x\) and \(y\), is simply \(\sqrt{(x_0 - y_0)^2 + (x_1 - y_1)^2 + \cdots + (x_{d-1} - y_{d-1})^2}\), where \(d\) is the dimensionality of the observations. In our case \(d=2\) which is why we only have \(x_0\) and \(x_1\). Also, since we’re only using the distances for comparative purposes, it’s not even necessary to take the square root. In step 2, the centroid is simply the sum of all the points divided by the number of points.
Implementation
First, a little housekeeping before getting to the implementation of the algorithm.
10 HOME : VTAB 21
20 PI = 3.14159265
30 GOSUB 1000 : REM DRAW AXIS
40 GOSUB 100 : REM GENERATE DATA
50 GOSUB 900 : REM WAIT FOR KEY
60 GOSUB 2000 : REM RUN K-MEANS
70 END
100 REM == HYPERPARAMETERS ==
...
450 DIM P%(2,1) : REM RANDOM POINTS
460 REM == K-MEANS DATA TABLES ==
470 DIM DI(NS - 1,KN - 1)
480 REM -- K - MU-XO, MU-X1, N-K --
490 DIM KM(KN - 1,2)
500 REM -- K - OLD MU-X0, OLD MU-X1 --
510 DIM KO(KN - 1,1)
...
900 REM == WAIT FOR KEYSTROKE ==
910 POKE 49168,0 : REM CLEAR BUFFER
920 IF PEEK(49152) < 128 GOTO 920
930 POKE 49168,0
940 RETURN
At the very top of the program I decided to organize everything into subroutines. The idea here is to enable expansion into other ML algorithms.
The “wait for key” subroutine is the APPLESOFT BASIC method for simply waiting for any keystroke before continuing. (PEEK and POKE are commands for directly accessing addresses in memory. I had those numbers memorized in high school but, naturally, I had to look them up.) I thought it’d be nice to add this pause after generating the data but I might take it out later.
Lastly, at the end of the “hyperparameters” section I declare a convenience array, P%(2,1) to keep track of 3 random points as well as a few arrays I’m going to use in the k-means algorithm. The reason I do this here is because in APPLESOFT BASIC you get an error if you declare an array that already exists. Should at some point I want to call the k-means algorithm multiple times, this won’t be a problem.
Initialize
Getting started, the first thing to do is initialize the algorithm by generating \(k\) cluster centroids. (\(k\) is a hyperparameter that specifies the number of clusters to be “found.” I set it previously with KN = 2.)
2000 REM == K-MEANS ==
2010 PRINT "RUN K-MEANS"
2020 REM -- CLEAR PREDICTIONS --
2030 FOR I = 0 TO NS - 1
2040 DS%(I,3) = 0
2050 NEXT I
2100 REM -- INITIALIZE CENTROIDS --
2110 FOR I = 0 TO KN - 1
2120 J = INT(RND(1) * NS)
2130 IF DS%(J,3) = 1 GOTO 2120
2140 KM(I,1) = DS%(J,1)
2150 KM(I,2) = DS%(J,2)
2160 DS%(J,3) = 1
2170 NEXT I
2200 REM -- DRAW LINES BETWEEN CENTROIDS --
2210 FOR I = 1 TO KN - 1
2220 HPLOT KM(I-1,0), 159-KM(I-1,1) TO KM(I,0), 159-KM(I,1)
2230 NEXT I
2240 GOSUB 3000: REM DRAW DECISION BOUNDARY
I start by clearing out the prediction column, \(y\), of the dataset table, DS%(NS - 1,3) because I’m going to use this to make sure I don’t randomly pick the same point twice. Then for each class I randomly pick a point from the dataset. If it’s already been used I randomly pick another. KM(KN - 1, 2) is where I store the means for each cluster along with a count of the number of points in each cluster.
Finally, I draw a line between the cluster centroids. This loop does not take into account all combinations of centroids (it works fine if \(k=2\)) and generates an error if a centroid is off the screen, which is possible, so I might just get rid of this later, since it’s not really necessary, rather than try to fix it.
Step 1 - Assignment
The fist step is to assign every data point to the nearest cluster centroid.
2300 REM -- COMPUTE ASSIGNMENTS --
2310 FOR I = 0 TO NS - 1
2320 PRINT "POINT ";I;" AT ";DS%(I,0);",";DS%(I,1);
2330 DS%(I,3) = 0
2340 FOR J = 0 TO KN - 1
2350 DI(I,J) = (DS%(I,0)-KM(J,0))^2 + (DS%(I,1)-KM(J,1))^2
2360 IF J >0 AND (DI(I,J) < DI(I,DS%(I,3))) THEN DS%(I,3) = J
2370 NEXT J
2380 PRINT " -> ";DS%(I,3);" Y^=";DS%(I,2)
2390 NEXT I
2500 REM -- COMPUTE ACCURACY --
2510 CT = 0
2520 FOR I = 0 TO NS - 1
2530 IF DS%(I,2) = DS%(I,3) THEN CT = CT + 1
2540 NEXT I
2550 A = CT / NS
2560 IF A < 0.5 THEN A = 1 - A
2570 PRINT "ACCURACY = "; INT(A*10000+0.5)/100;"%"
The assignment step is also quite easy. I loop through all the data points, computing the Euclidean distance to each cluster centroid. (Since SQRT() is expensive, and unnecessary here since we’re just comparing, I actually just compute the square of the Euclidean distance.) If the distance is less than the previous minimum distance, DI(I,DS%(I,3)), I update the assignment, DS%(I,3) = J.
At the end, I compute the accuracy of the computed assignments by simply counting the number of assignments, DS%(I,3), that match the actual labels, DS%(I,2). Here, however, there’s an interesting wrinkle: with two classes, half the time the label I choose for the assignment is the opposite of the label from the original dataset. K-means doesn’t require the distinction, so at times I was seeing a perfect classification reporting 0% accuracy. The line IF A < 0.5 THEN A = 1 - A addresses this, however, it only works for 2 classes. I’ll need something more robust should I want this to work for \(k > 2\).
Step 2 - Update
The second step is to recompute the cluster centroids based on the assigned data points. Convergence occurred if the centroids don’t change (within a tolerance) from the previous iteration.
2600 REM -- COMPUTE CENTROIDS --
2610 FOR J = 0 TO KN - 1
2620 K0(J,0) = KM(J,0)
2630 K0(J,1) = KM(J,1)
2640 KM(J,0) = 0: KM(J,1) = 0
2650 KM(J,2) = 0
2660 NEXT
2670 FOR I = 0 TO NS - 1
2680 Y = DS%(I,3)
2690 KM%(Y,0) = KM%(Y,0) + DS%(I,0)
2700 KM%(Y,1) = KM%(Y,1) + DS%(I,1)
2710 KM%(Y,2) = KM%(Y,2) + 1
2720 NEXT
2730 FOR I = 0 TO KN - 1
2740 KM%(I,0) = KM%(I,0) / KM%(I,2)
2750 KM%(I,1) = KM%(I,1) / KM%(I,2)
2760 NEXT
2800 REM -- DETERMINE CONVERGENCE --
2810 DI = 0
2820 FOR I = 0 TO KN - 1
2830 DI = DI + (KM%(I,0) - KO%(I,0)) ^ 2 + (KM%(I,1) - KO%(I,1)) ^ 2
2840 NEXT
2850 IF DI > 0.01 THEN GOTO 2200
2860 PRINT "K-MEANS CONVERGED"
2900 REM -- CLEAR GRAPHICS AND REDRAW WITH DECISION BOUNDARY --
2910 GOSUB 1000
2920 FOR I = 0 TO NS - 1
2930 X0% = DS%(I,0)
2940 X1% = DS%(I,1)
2950 K = DS%(I,2)
2960 ON K + 1 GOSUB 1200,1300
2970 NEXT
2980 GOSUB 3000
2990 RETURN
I start by saving the cluster centroids to KO(KN - 1,1). This is used later to determine convergence. I then iterate through ever data point, adding it’s values to the cluster to which it belongs while keeping track of the number of data points in each cluster. Next I iterate through each cluster and compute the mean of each dimension by dividing by the number of data point in that cluster.
Lastly, I determine if there’s convergence by measuring how far all the centroid have moved. (Again, I don’t bother with the SQRT().) If the answer is more than the specified tolerance, \(0.01\), I go back to Step #1. Otherwise, I clear the graphics, redraw the axis and data points and finish by drawing the decision boundary.
Drawing the decision boundary
This code is a slog and it’s not really critical to understanding ML but I thought it’d be cool to drawn a decision boundary while k-means is iterating and then again at the end. Given a point (the midpoint on the segment between two cluster centroids) and a slope (which is perpendicular to that segment), the challenge is to drawn a line inside the ‘box’ of the screen, assuming the line intersects that box.
3000 REM -- DRAW DECISION BOUNDARY --
3010 FOR I = 1 TO KN - 1
3020 M = 1E6
3030 IF KM%(I - 1,1) - KM%(I,1) <> 0 THEN M = -1 * (KM%(I - 1,0) - KM%(I,0)) / (KM%(I - 1,1) - KM%(I,1))
3040 P%(0,0) = (KM%(I,0) - KM%(I - 1,0)) / 2 + KM%(I - 1,0)
3050 P%(0,1) = (KM%(I,1) - KM%(I - 1,1)) / 2 + KM%(I - 1,1)
3060 GOSUB 3080
3070 NEXT
3080 REM -- DRAW LINE FROM SLOPE AND POINT --
3090 NX = 1 : REM -- REM NUMBER OF INTERSECTIONS --
3100 IF ABS(M) > 1E5 THEN GOSUB 3240 : GOTO 3210 : REM VERTICAL LINE
3110 P%(NX,1) = M * (10 - P%(0,0)) + P%(0,1)
3120 IF P%(NX,1) > 10 AND P%(NX,1) < 149 THEN P%(NX,0) = 10 : NX = NX + 1
3130 P%(NX,1) = M * (269 - P%(0,0)) + P%(0,1)
3140 IF P%(NX,1) > 10 AND P%(NX,1) < 149 THEN P%(NX,0) = 269 : NX = NX + 1
3150 IF NX = 3 THEN GOTO 3210
3160 IF M <> 0 THEN P%(NX,0) = (10 - P%(0,1)) / M + P%(0,0)
3170 IF M <> 0 AND P%(NX,0) > 10 AND P%(NX,0) < 269 THEN P%(NX,1) = 10 : NX = NX + 1
3180 IF NX = 3 THEN GOTO 3210
3190 IF M <> 0 THEN P%(NX,0) = (149 - P%(0,1)) / M + P%(0,0)
3200 IF M <> 0 AND P%(NX,0) > 10 AND P%(NX,0) < 269 THEN P%(NX,1) = 149 : NX = NX + 1
3210 REM -- DRAW LINE --
3220 IF NX = 3 THEN HPLOT P%(1,0),159 - P%(1,1) TO P%(2,0),159 - P%(2,1)
3230 RETURN
3240 REM -- VERTICAL LINE --
3250 P%(1,0) = P%(0,0)
3260 P%(2,0) = P%(0,0)
3270 P%(1,1) = 10
3280 P%(2,1) = 269
3290 RETURN
Without delving too far into the details, this routine relies heavily on the convenience array, P%(2,1), that I declared during the “hyperparameters” routine. I start by computing the slope of the perpendicular segment connecting two centroids. I then find the midpoint of that segment. (By the way, this routine also does not account for all combinations of centroids, but it works when \(k=2\).) I accommodate for when the slope is vertical and use P%(0,0) and P%(0,1) to store the midpoint between the two centroids and M for the slope.
I then iterate through the 4 sides of the ‘box’ on the screen, using the corners (10,10) and (269,149) so that the decision boundary isn’t drawn all the way to the edges of the screen. I thought that would look prettier this way. I next determine if the decision boundary intersects, respectively, the left, right, top and bottom edges of the box. I use NX to keep track of the number of sides of the box intersected by the decision boundary and P%(NX,0) and P%(NX,1) to keep track of those intersections. If NX = 3, which means there are two intersections, I draw the line because it’s inside the box.
Can we do better?
Yes! Yes, we can.
While k-means is simple, it does not take advantage of our knowledge of the Gaussian nature of the data. If we know that the distributions are at least approximately Gaussian, which is frequently the case, we can employ a more powerful application of the Expectation Maximization (EM) framework (k-means is a specific implementation of centroid-based clustering that uses an iterative approach similar to EM with ‘hard’ clustering) that takes advantage of this. This post is already long enough, so we’ll deal with that another day. Eventually, perhaps, we’ll also get to deep learning, although developing back propagation for an arbitrary size neural net using APPLESOFT BASIC on an Apple ][+ is not going to be easy.
Social media sharing
I shared this post on Hacker News and, to my surprise and delight, got a decent amount of feedback, including some helpful corrections.
My post on Facebook received significantly less reaction. My friends are apparently a lot less interested in ML algorithms on retro hardware than randos on Hacker News. My share requests to Facebook groups Apple II Enthusiasts and Retro Microcomputers were both rejected, which is a bit disappointing. Still, those are fun groups to follow. My post on the VCF forum also got zilch. (I attend the Vintage Computer Festival at the Computer History Museum, which was a good time.) Perhaps I’ll try Reddit and LinkedIn next to see what happens…

 Google Scholar
Google Scholar

Leave a Comment