The Perceptron Class

What is a Perceptron?

The node is the ‘atomic’ unit of a neural network and the Perceptron is the most basic form of node. Wikipedia describes it as an ‘algorithm,’ but you can also think of it as an ‘object’ that accepts some inputs and produces an output. Neural networks may then be constructed by stringing Perceptrons together and potentially stacking layers of them on top of each other. With enough of them, what they can end up doing is, often, nothing short of magic.

Walking through the diagram below, a Perceptron will accept any number (\(n\), for example) of inputs, \(x_0\) to \(x_n\), and product a single output, \(y\). These inputs are, of course, numbers, although they may be arbitrarily large or small and include fractions. Each input is then multiplied by a weight, \(w_0\) to \(w_n\). The summation of all the inputs multiplied by their weights is called the hypothesis:

\[h(X) = x_0 w_0 + x_1w_1 + \cdots +x_nw_n\]

The hypothesis is thus a single number which is then sent through an activation function. There are many types of activation functions (we’ll review some later), but the simplest is the “step”: if the hypothesis is positive or zero our output is 1, otherwise it is 0.

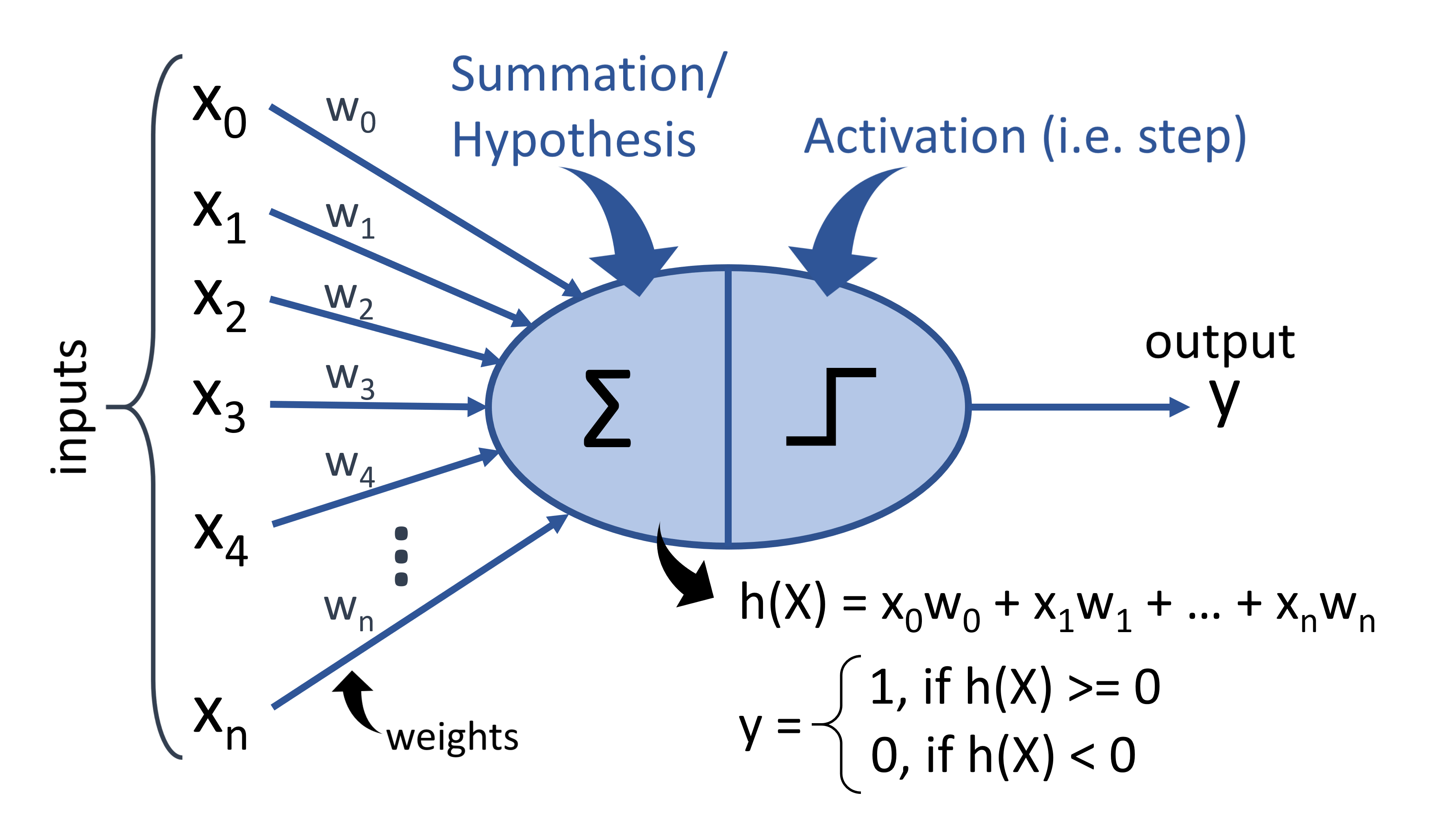
So what’s the point of this? We’ll dig into that, but at a high level what we’ve got is a linear classifier that simply checks to see if our hypothesis is either positive or negative. The key here, which we’ll explore through a process called “training,” is to determine the ‘right’ weights to make the Perceptron appropriately classify the inputs. That’s what makes the magic: finding the weights.

The Perceptron Class

We’re going to use Python because it easy to learn, easy to use and has become, more or less, for reasons associated with data science-related libraries, the language of choice for people building neural networks. That being said, you could follow these exercises using most any object-oriented programming language.

As mentioned in the Motivation, this is the thing that, for performance reasons, nobody ever does. To reiterate, we’re doing it to try to get insights into functioning of Perceptrons and neural networks.

Below is the first chuck of code we’ll need. We define the Perceptron call and set up the initialization function to accept the number of inputs. For the moment, there’s nothing else to define. Using the number of inputs we then create an equal number of weights to which we’ll assign random floating point numbers between -1 and +1.

import random # We'll need this to generate random numbers
    
class Perceptron: # This begins the class definition
        
    # This runs whenever we instantiate
    def __init__(self, num_inputs):
        # Create an empty array for the weights
        self.weights = []
        for _ in range(0, num_inputs):
            # Set each weight to a random number from -1 to +1
            # random.random() produces a floating point number in the range [0.0, 1.0)
            self.weights.append(random.random() * 2 - 1)
        # Print the weights to see what happened
        print(self.weights)

Now if you run a = Perceptron(5), which creates a new Perceptron with 5 inputs, called a, you should get an output like [0.12754034043801643, -0.20861593234059006, -0.37130273318835005, -0.10781144821380861, -0.5746109925723668], which is simply an array of 5 random numbers between -1 and +1. So the first step works.

Here is the next text.

Here is some more text.