Refactoring

Well, that didn’t take too long. When I was developing Mortal Wayfare, I recall frequently passing hours just looking at the code, trying to figure out how to better represent what I was trying to accomplish while improving the organization. (Should this method go in a different class? Is there a better name for this variable? Should I break this code out into a function?…) Some days I would do nothing but this. Having never been a professional software developer, I’m not sure to what extent this is normal, but I found the process to be very helpful.

I suppose there’s a balance between planning out what you’re going to do and just getting started. For my this project, I leaned toward the latter. As such, after the first pass I already decided to change it up. More specifically, the first thing I decided to do was, rather than have a different array for each class of data, move everything into a single array. The reason is that, during training, this will facilitate looping over all the data.

Quick note on line numbers: refactoring BASIC almost always consists of changing line numbers. As such, this code is not going to match up with previous posts. Hopefully that won’t be confusing.

Refactoring the hyperparameters

To make that happen, I start by moving all of my generator hyperparameters into a single array, GE(..,..), where the first axis is the class. The second axis contains, respectively, \(u_{x_0}, u_{x_1}, \sigma_{x_0}, \sigma_{x_1}, \rho\) and \(\sqrt{1 - \rho^2}\). (See Synthesizing data - Box-Muller for details.) The last element is purely for performance since this quantity will be needed frequently. (Upon further refection, I could have used \(\sqrt{1 - \rho^2} \sigma_{x_1}\) but this is a small optimization for later.)

100 REM == HYPERPARAMETERS ==
110 KN = 2: REM # OF CLASSES
120 DIM KN%(KN - 1): REM # OF SAMPLES FROM EACH CLASS
130 KN%(0) = 100
140 KN%(1) = 50

150 REM -- GENERATORS --
160 REM -- CLASS - MU-X0, MU-X1, SIG-X0, SIG-X1, RHO --
170 DIM GE(KN - 1,4)

180 REM -- CLASS 0 --
190 GE(0,0) = 100: REM MU-X0
200 GE(0,1) = 50: REM MU-X1
210 GE(0,2) = 30: REM SIG-X0
220 GE(0,3) = 10: REM SIG-X1
230 GE(0,4) = 0.5: REM RHO
240 GE(0,5) = SQR(1 - GE(0,4) ^ 2)

250 REM -- CLASS 1 --
260 GE(1,0) = 200: REM MU-X0
270 GE(1,1) = 100: REM MU-X1
280 GE(1,2) = 50: REM SIG-X0
290 GE(1,3) = 25: REM SIG-X1
300 GE(1,4) = -0.5: REM RHO
310 GE(1,5) = SQR(1 - GE(1,4) ^ 2)
320 REM == END HYPERPARAMETERS ==

Note: here is a funny thing with Applesoft BASIC arrays. I couldn’t remember if there was 0- or 1-indexed. Turns out, they are both! DIM A(3) will create an array of length 4 which goes from index 0 to 3. I can’t recall seeing anything like that anywhere else. So, I use DIM GE(KN-1,4) because I want the first axis to have KN elements and the second axis to have 5. Funny.

Another note: Applesoft BASIC only uses the first two characters of a variable names, however, KN and KN%(..) are considered different.

Generating the samples

After counting up the total number of samples, I then create DS%(..,..) which replaces AX%(..) and BX%(..). The first axis contains the samples, of which there are NS in total. The second axis is, respectively, \(x_0, x_1, \hat{y}\) and \(y\). \(\hat{y}\) is the label (i.e., the class) and \(y\) is the prediction, which we’ll get to later. Having all the data in a single array will facilitate generating and training.

330 NS = 0: REM TOTAL # SAMPLES
340 FOR I = 0 TO KN - 1
350   NS = NS + KN%(I)
360 NEXT

370 REM -- DATA TABLE --
380 REM -- # - X0, X1, Y-HAT, Y --
390 DIM DS%(NS - 1,3)

Since I’d like for my data to be randomly sampled, rather than scrambled after the fact, I decided to use ‘adaptive quota sampling’ to generate them randomly while ending up with the appropriate quantities. I could have simply taken the end proportion of each class and use that to create probabilities during generation but then there would be no guarantee then the final number of samples for each class would be correct.

400 REM -- REMAINING SAMPLES COUNT --
410 DIM RK%(KN - 1)
420 FOR I = 0 TO KN - 1
430   RK%(I) = KN%(I)
440 NEXT

450 REM == GENERATE SAMPLES ==
460 FOR I = 0 TO NS - 1
470   REM -- ADAPTIVE QUOTA SAMPLING --
480   REM -- PICK CLASS BASED ON REMAINING SAMPLES TO GENERATE --
490   P% = RND(1) * (NS - I)
500   CS = 0
510   J = 0
520   CS = CS + RK%(J)
530   K = J
540   J = J + 1
550   IF P% >= CS GOTO 520
560   RK%(K) = RK%(K) - 1
570   REM -- GENERATE RANDOM NORMAL VARIABLES Z0, Z1 --
580   GOSUB 1400
590   REM -- GENERATE SAMPLE FROM Z0, Z1 --
600   REM X0 = MU-X0 + SIG-X0 * Z0
610   X0% = GE(K,0) + GE(K,2) * Z0
620   REM X1 = MU-X1 + RHO * SIG-X1 * Z0 + SQR(1 - RHO^2) * SIG-X1 * Z1
630   X1% = GE(K,1) + GE(K,4) * GE(K,3) * Z0 + GE(K,5) * GE(K,3) * Z1
640   DS%(I,0) = X0%
650   DS%(I,1) = X1%
660   DS%(I,2) = K
670   PRINT I + 1; TAB(5); "SAMPLE "; KN%(K) - RK%(K);
680   PRINT TAB(16); "IN CLASS "; K;
690   PRINT " AT ("; X0%; ","; X1%; ")"
700   ON K + 1 GOSUB 1200,1300: REM PLOT SAMPLE
710 NEXT

RK%(..) holds the remaining number of samples to be generated for each class. Lines 490 to 550 then produce a random number P% which is from 0 to the number of remaining samples to generate and then figures out which class this should be based on the remaining number of samples to be generated for each. The beauty of this is that the probably of generating a sample in each class will be a function of how many remaining samples need to be generated. It took a while to debug, but in the end this produces exactly the number of samples in each class as specified in the hyperparameters.

The code from lines 580 to 690 is the same as previously, however, the class-specific variables have been replaced by GE(..,..), as mentioned above. Also, I changed X% and Y% to XO% and X1% to avoid confusion and be more consistent with the \(Y = \theta^T X\) literature.

Line 700 is nifty. I don’t recall using ON..GOSUB in high school but it enables branching based on the argument. I use K+1 since the first class is \(0\) and a zero argument doesn’t branch. For the moment, this only supports two classes.

Counting the samples

For debugging purposes, I added some code to count the number of samples in each class to make sure it matched the hyperparameters. In the end, I decided to leave it. The loop is actually a bit slow but it’s only run once.

720 REM == COUNT SAMPLES OF EACH CLASS TO VERIFY RESULT ==
730 DIM CT%(KN - 1)
740 FOR I = 0 TO NS - 1
750   K = DS%(I,2)
760   CT%(K) = CT%(K) + 1
770 NEXT
780 PRINT "TOTAL SAMPLES FOR EACH CLASS:"
790 FOR I = 0 TO KN - 1
800   PRINT CT%(I); TAB(5); "SAMPLES IN CLASS "; I
810 NEXT
820 END

Fixing the plotting routines

The only remaining tweaks were for the plotting routines. The two routines below, which are called from the ON..GOSUB in line 700, are updated to use XO% and X1%. The rest is the same.

1200 REM == DRAW + AT X0, X1 ==
1210 X1% = 159 - X1%
1220 IF X0% < 1 OR X0% > 270 THEN RETURN
1230 IF X1% < 1 OR X1% > 150 THEN RETURN
1240 HPLOT X0% - 1,X1% TO X0% + 1,X1%
1250 HPLOT X0%,X1% - 1 TO X0%,X1 + 1
1260 RETURN

1300 REM == DRAW BOX AT X0, X1 ==
1310 X1% = 159 - X1%
1320 IF X0% < 1 OR X0% > 270 THEN RETURN
1330 IF X1% < 1 OR X1% > 150 THEN RETURN
1340 HPLOT X0% - 1,X1% - 1 TO X0% + 1,X1% - 1
1350 HPLOT X0% - 1,X1%: HPLOT X0% + 1,X1%
1360 HPLOT X0% - 1,X1% + 1 TO X0% + 1,X1% + 1
1370 RETURN

Testing Irwin-Hall as an alternative to Box-Muller

The final chunk of code is interesting. After sharing my Box-Muller routine with my friend, Răzvan Surdulescu, he suggested using the Irwin-Hall Distribution. SQR and COS are expensive operations in BASIC and Irwin-Hall approximates a normal distribution by sampling 12 uniform random numbers.

1400 REM == IRWIN-HALL DISTRIBUTION ==
1490 Z0 = -6:Z1 = -6
1500 FOR I = 1 TO 12
1510   Z0 = Z0 + RND(1)
1520   Z1 = Z1 + RND(1)
1530 NEXT
1540 RETURN
1550 REM == RANDOM GEN SPEED TEST ==
1560 FOR I = 1 TO 500
1570   GOSUB 1400
1580 NEXT

I gave it a go and ran a comparison by generating 500 pairs of random numbers with each. This took 63s with Box-Muller and 90s with Irwin-Hall, so I will stick with the former. That being said, this was a nifty idea.

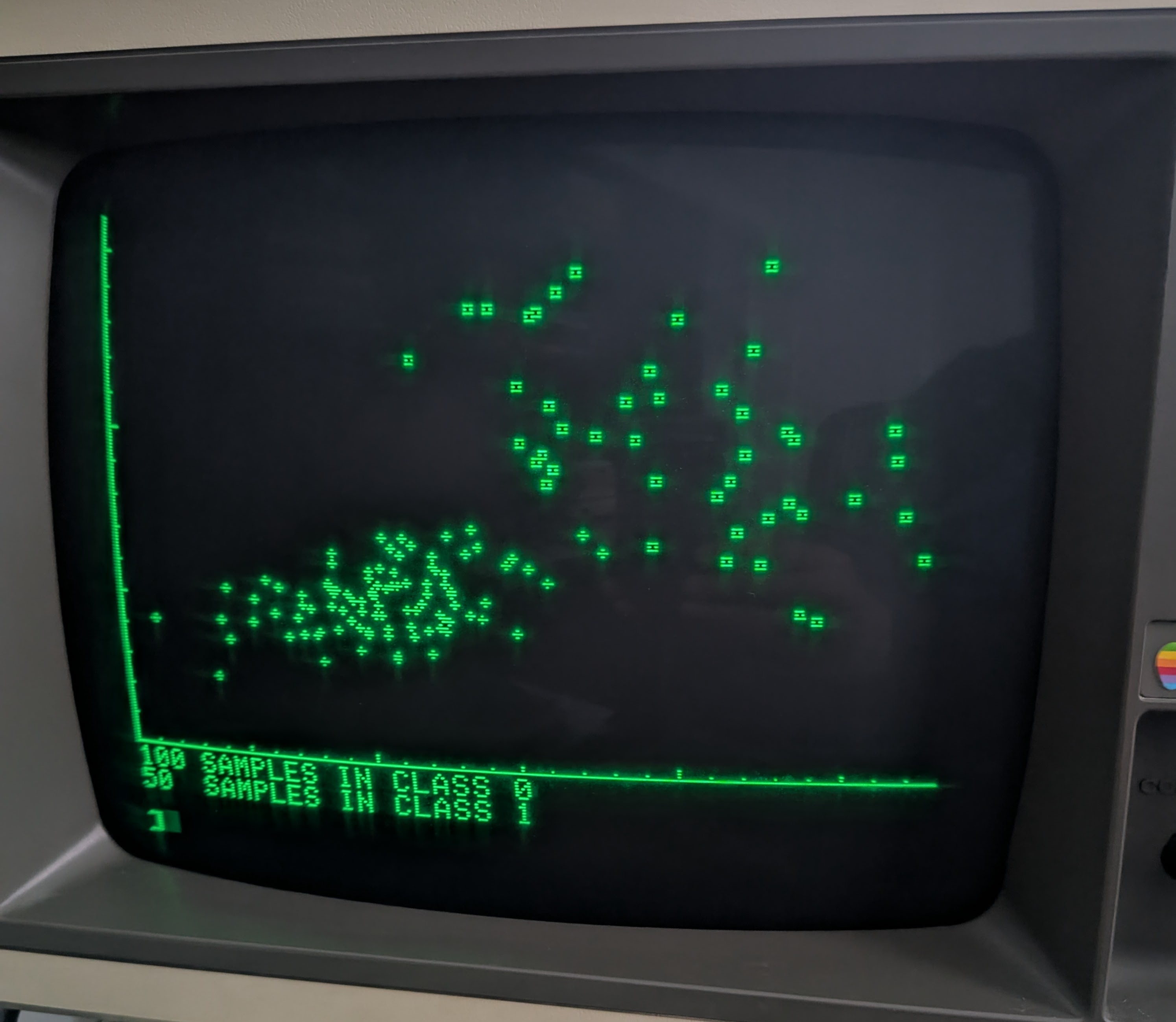
An updated final plot

The final result looks pretty much the same as before but it’s flipped horizontally. The new data structure, however, will make implementing ML much easier.

Now onto implementing the simplest and easiest to understand machine learning algorithm…